Los tipos de ecuaciones diferenciales ordinarias de primer orden son las ecuaciones diferenciales más estudiadas debido a su amplia aplicabilidad en diversas áreas de la ciencia y la ingeniería. Estas ecuaciones permiten modelar fenómenos que involucran tasas de cambio y son la puerta de entrada al fascinante mundo de la modelización matemática.

| Sección | Resumen |
|---|---|
| Tipos de ecuaciones Diferenciales ordinarias de primer orden | Conoce los 10 tipos de EDs lineales y no lineales más importantes para el modelado matemático |
| Estrategias de solución para cada tipo de ED de 1er orden | Entiende gráficamente la estrategias seguidas para resolver la mayoria de las EDs |
| Ejemplos de cada tipo de EDs ordinarias de 1er orden | Repasamos cada tipo de ED ordinaria de primer orden |
| Homogéneas y Separables | Forma estándar, explicación sucinta del método de solución y ejemplos resueltos paso a paso |
| Lineales y Exáctas | Forma estándar, explicación sucinta del método de solución y ejemplos resueltos paso a paso |
| Directa y por Sustitución | Forma estándar, explicación sucinta del método de solución y ejemplos resueltos paso a paso |
| Riccati y Bernoulli | Forma estándar, explicación sucinta del método de solución y ejemplos resueltos paso a paso |
| Lagrange y Clairaut | Forma estándar, explicación sucinta del método de solución y ejemplos resueltos paso a paso |
| Comparaciones | Repaso de metodos y estrategias de las EDs lineales no – lineales |
| Resumen cuadro sinóptico: clasificación y métodos de solución | Tipos, formas estándar y métodos de solución resumidos enun cuadro sinóptico |
| Conviertete en expert@ | Oportunidad para tu transformación hacia la maestría |
| Explora nuestros Cursos Exclusivos en linea | Tenemos TODO para que te conviertas en un expert@ en Ecuacions Diferenciales con Inteligencia Artificial. Inscríbete a nuestros cursos y recibe actualizaciones que te mantendrán en el pináculo de tu sector |
El conocimiento de sí mismo es el comienzo de toda sabiduría.
~Aristóteles
Tipos de ecuaciones diferenciales ordinarias de primer orden
En general las ecuaciones diferenciales se clasifican por tipo, orden y linealidad. De moso que, las ecuaciones diferenciales pueden ser:
- Según su tipo: ordinarias o parciales,
- Según su orden: de primer orden o de orden superior y
- Según su linealidad: lineales y no-lineales.
Las ecuaciones diferenciales ordinarias son aquellas donde las derivadas de la ecuación solo dependen de una variable independiente, mientras las ecuaciones diferenciales parciales, sus derivadas son parciales, es decir, depende de mas de una variables independientes.
Clasificación según su tipo
Ejemplos de ecuaciones diferenciales ordinarias:
$$\frac{dy^{2}}{dx^{2}}+x^{2}\frac{dy}{dx}+x=xy^{2}$$
$$\frac{d^{4}y}{dx^{4}}+x^{2}\frac{d^{3}y}{dx^{3}}+x^{3}\frac{dy}{dx}=xe^{x}$$
$$xy’+y=3$$
$$y^{´´´}+2\left(y^{´´}\right)^{2}+y’=0$$
$$y^{´ ´}-y = \cos{(x)}$$
$$\left( \frac{d^{2}y}{dx^{2}}\right)^{2}-x\frac{dy}{dx}+5y=n$$
$$\frac{d^{2}x}{dt^{2}}-\mu\left( 1-x^2\right)\frac{dx}{dt}=0$$
Ésta última ecuación es la ecuación de Van de pol y representa una cuación diferencial ordinaria de segundo orden.
Podemos notar que la derivada de $y$, solo depende de la variable independiente $x$ en cada caso, escepto la ecuación de Van der Pol, donde la función $y$ depende de $t$, únicamente. Las ecuaciones donde las derivads se expresan con la tilde, generalmente son funciones de $x$, a menos que se exprese lo contrario.
Ejemplos de ecuaciones diferenciales parciales:
$$\frac{\delta y}{\delta t}-\alpha^2\frac{\delta y}{\delta x}=e^{x}$$
$$\frac{\delta^{2} u}{\delta x^{2}}+\frac{\delta^{2} u}{\delta t^{2}}=x^{2}+y$$
$$\left( \frac{\delta x}{\delta t}\right)^{3}+\frac{\delta^{3}x}{\delta v^{3}}+2=\left( \frac{\delta^{2}}{\delta v\delta t}\right)^{3}$$
$$\frac{\delta u}{\delta t}+\frac{\delta^{3}u}{\delta x^{3}}-6f(t)u\frac{\delta u}{\delta x}=g\left(t,u\right)$$
Ésta ultima ecuación parcial llamada: ecuación de Korteweig-de Vries (kdV), ha sido usada para modelar el comportamiento de ondas en aguas poco profundas.
Aquí, podemos notar que la derivada parcial de $y$, depende tanto de la variable independiente $t$ como de la variable independiente $x$.
Tipo de ecuación diferencial según el orden de su derivada
Las ecuaciones diferenciales de primer orden, son aquellas donde el orden máximo al que está elevado sus derivadas es 1, mientras que las de orden superior, puede tener otras derivadas elevadas a diferentes ordenes y el mayor de ellos en la ecuación, determinara el orden de la ED.
Ejemplos de ecuaciones diferenciales de primer orden:
$$F\left(x,y,y’\right)=0$$
$$\frac{dy}{dx}=x+y$$
$$y’-y =0$$
En ambos ejemplos vemos que la ecuación diferencial solo tiene una derivada y ésta es de orden 1. Como hemos mencionado, las ecuaciones donde las derivads se expresan con la tilde, generalmente son funciones de $x$, a menos que se exprese lo contrario.
Ejemplos una ecuaciones diferenciales de segundo orden:
$$F\left(x,y,y’,y^{´ ´}\right)=0$$
$$\frac{dy^{2}}{dx^{2}}+(x-y)y=0$$
$$\frac{d^{2}y}{dt^{2}}+5\frac{dy}{dt}+6y=0$$
Ejemplos de ecuaciones diferenciales de tecer orden:
$$F\left(x,y,y’,y^{´ ´},y^{´´ ´}\right)=0$$
$$3x^{3}y^{´ ´ ´}-5xy^{´´ }+6y’-7y=0$$
$$\frac{d^{3}y}{dx^{3}}+2\frac{d^{2}y}{dx^{2}}=\sec{(x)}$$
Una ecuación diferencial de orden $n$, se representa:
$$F\left(x,y,y’,y^{´ ´},…,y^{n}\right)=0$$
Clasificación según su linealidad
Ecuaciones diferenciales lineales
Las ecuaciones diferenciales lineales ordinarias, son aquellas donde los coeficientes de la variable dependiente ($V$ o $y$ en los ejemplos que vienen abajo), son solo dependientes de la variable independiente o constantes y donde ésta variable dependiente y todas sus derivadas son de primer grado, de modo que:
Ejemplos de ecuaciones lineales, ordinarias de primer orden:
$$C\frac{dV}{dt}=I_e-I_i$$
$$\frac{dy}{dx}-y=2\left( 1-x\right)$$
Ejemplos de ecuaciones lineales, ordinarias, de segundo orden:
$$\frac{d^{2}x}{dt^{2}}+4\frac{dx}{dt}+x=\cos{(x)}^{3}$$
$$t^{2}\frac{d^{2}x}{dt^{2}}+t\frac{dx}{dt}+\left(t^{2}-\alpha^{2} \right)x=0$$
Ecuación diferencial lineal de orden $n$:
$$a_n(x)\frac{d^{n}y}{dx^{n}}+a_{n-1}\frac{d^{n-1}y}{dx^{n-1}}+a_{n-2}(x)\frac{d^{n-2}y}{dx^{n-2}}+…+a_0(x)y=0$$
Donde: $a_n$,$a_{n-1}$,$a_{n-2}$,…,$a_0$, son funciones de x.
Ecuaciones diferenciales no-lineales
La ecuaciones diferenciales no-lineales ordinarias, son aquellas donde los coeficientes de su variable dependiente y no solo dependen de su variable independiente x y que su propia variable dependiente puede estar elevada a grados mayor a uno o pertenecer a funciones no lineales como $\sin$ y $\cos$.
Ejemplos de ecuaciones no-lineales, ordinarias, de primer orden:
$$y’=y^{2}-x^{2}$$
$$\frac{dy}{dx}=xy^{2}$$
Ejemplos de ecuaciones no-lineales, ordinarias, de segundo orden:
$$\frac{d^{2}\theta}{dt^{2}}+\frac{g}{l}\sin{(\theta)}=0$$
y
$$m\frac{d^{2}x}{dt^{2}}+kx^{2}=0$$
Ejemplo de ecuación no-lineal ordibnaria de tercer orden:
$$\frac{d^{3}y}{dx^{3}}+y^{2}=0$$
Estrategias de solución para cada tipo de ecuaciones diferenciales ordinarias de primer orden
En la gráfica de abajo se puede notar el camino que generalmente se sigue al resolver las EDs mostradas.

La estrategia es tratar de reducir la ED a una versión mas facilmente integrable.
Ejemplo de secuencia de solución para la ED de Riccati, según el gráfico anterior
Por ejemplo, las Ecuaciones Diferenciales de Riccati, que en realidad es un tipo de ecuación diferencial no-lineal, pues la variable dependiente está elevada a grado 2 (ver sección: Riccati, mas adelante), se puede resolver siguiendo la trayectoria ascendente de la Figura 2, anterior de la siguiente forma:
- Reducimos la ED de Riccati a un ED de Bernoulli, mediante una sustitución (tambien se puede reducir a un ED lineal directamente).
- Reducimos mediante otra sustitución a un ED lineal a partir de la de Bernoulli
- Obtnemos un Factor Integrante (F.I.)
- Convertimos a una ED separable al multiplicar el F.I.
- Interamos las EDs direactas resultantes
- Obtenemos la sunción solución buscada de la integración anterior.
Para ver ejemplo paso a paso sobre la ecuación diferencial de Riccati, puede dirigirse a nuestro artículo: Ecuaciones Diferenciales No-Lineales: Riccati, Ejercicios Resueltos.
Los pasos anteriore son una versión extendida o paso a paso para solucionar la ED de Riccati (conociendo una solución previa), que puede ser simplificada como lo puedes ver el en enlace anterior a los ejemplos resueltos de Riccati.
Construye tus propios algoritmos utilizando las trayectorias anteriores
Siguiendo cualquiera de las trayectorias del gráfico anterior, puedes construir el algoritmo de solución de cualquiera de las EDs aquí estudiadas. Teinvito a realizarlo y que los compartas en la sección de comentarios que encuentras al final del artículo. (y)
A continuación, se describen todos los 10 tipos de ecuaciones diferenciales ordinarias de primer orden, más importantes, describiendolas en pares, poniéndolas por su relvancia en orden decendente, y puntualizando sus características más distintivas: su forma estándar y sus métods de solución.
Ejemplos de tipos de ecuaciones diferenciales ordinarias de primer orden
Homogéneas y Separables
Separables

Forma estándar
Las ecuaciones diferenciales separables son aquellas que pueden expresarse como el producto de una función de $x$ y una función de $y$. Matemáticamente, toman la forma:
$$\frac{dy}{dx}=g(x)h(y)$$
donde: $g(x)$, $h(y)$, son funciones de $x$ y $y$, respectivamente.
Solución de las EDs sepables
La solución se obtiene al separar las variables y al integrar ambos lados de la ecuación.
$$\frac{dy}{h(y)}=g(x)dx$$
$$\int{\frac{dy}{h(y)}}=\int{g(x)}dx+C$$
Ejemplos resueltos
- $\frac{{dy}}{{dx}} = (1 + y^2) \tan (x)$
- $y^{e^{x}} {dy} – (e^{- y} + e^{2 x – y}) {dx} = 0$
- $\frac{dy}{(5-3y)^{2}} = \frac{dx}{2(4-x)^{2}}$
- $\sqrt{1-y^{2}}dx = \sqrt{1-x^{2}}dy$
- $\sin{(3x)}dx+2y \cos{(3x)}dy = 0$
Estos ejemplos los puedes encontrar desarrollados paso a paso en nuestro artículo: ECUACIONES DIFERENCIALES SEPARABLES.
Homogéneas

Forma estándar
Una ecuación diferencial de primer orden se denomina homogénea si puede escribirse en la forma:
$$\frac{dy}{dx}=f\left(\frac{y}{x}\right)$$
Donde f es una función de una sola variable.
Solución de las EDs homogéneas
Las ecuaciones homogéneas se pueden resolver mediante la sustitución:
$$v=\frac{y}{x}$$
que convierte la ecuación en una forma separable.
Ejemplos resueltos
- $\large 2x y \frac{d y}{d x} =4x^{2} +3y^{2}$
- $\large ( x-y ) d x+x d y=0$
- $\large ( x+y ) d x+x d y=0$
- $\large x d x+ ( y-2x ) d y=0$
- $\large y d x – 2 ( x+y ) d y=0$
- $\large ( y^{2} +y x ) d x+x^{2} d y=0$
Para saber como implementar paso a paso el algoritmo de solución de éste tipo de problemas consulta el siguiente artículo: Ecuacion Diferencial Homogenea 1er Orden.
Te recomiendo, nuestra presentación multimencionada en Academia.edu: Ecuacion Diferencial Homogenea de 1er orden. Concepto de homogeneidad, para que domines, de una vez por todas éste concepto. Ésta presentación te muestra de manera única y muy clara, qué significa el concepto de hogeneidad en las ecuacoines diferenciales de 1er orden.

Ambas ecuaciones, homogéneas y separables, comparten la característica de que pueden ser manejadas mediante manipulaciones algebraicas para alcanzar una forma en la que la integración es posible. La sustitución y la separación de variables son las claves para resolverlas.
Lineales y Exactas
Lineales
Forma estándar
Las ecuaciones diferenciales lineales de primer orden tienen la forma:
$$\frac{dy}{dx}+p(x)y=q(x)$$
Donde $p(x)$ y $q(x)$ son funciones conocidas de $x$. Estas ecuaciones se caracterizan por tener soluciones que pueden ser encontradas mediante el método del Factor Integrante.
Solución de las EDs lineales
Las ecuaciones diferenciales lineales de primer orden, pueden ser resueltas mediante hallar un factor integrante:
$$e^{\int{P(x)dx}}$$
Éste se multiplica por toda la la ecuación para reducirla a integraciones directas
Una explicación del origen de éste factor lo puede encontrar en éste artículo: De Donde sale el factor integrante.
Ejemplos resueltos:
- $$\large xy’+y={{e}^{x}}$$
- $ydx-4\left( x+{{y}^{6}} \right)dy=0$
- $\frac{dy}{dx}=5y$
- $\frac{dy}{dx}+y={{e}^{3x}}$
- ${{y}^{‘}}+3{{x}^{2}}y={{x}^{2}}$
Ejemplos resueltos de ecuaciones lineales paso a paso puedes verlos en el artículo: Ecuacion diferencial lineal de primer orden. (revisa la lista al final del mismo)
Empieza tu camino como expert@, modelando, y simulando problemas reales con ecuaciones diferenciales y programación y aumenta tu valor como ingeniero o profesional de las ciencias exactas aplicadas siendo un maestro en la resolución de problemas reales. Para eso te recmomiento nuestro artículo: Modelando la Concentración de una Sustancia en un Tanque con Entrada y Salida: El Modelo de Mezcla con un Tanque.

Exactas

Forma estándar
Una ecuación diferencial exacta de primer orden se presenta cuando existe una función $F(x,y)$ tal que su diferencial total coincide con la ecuación dada:
$$M(x,y)dx+N(x,y)dy=0$$
donde $M(x,y)=\frac{\delta F}{\delta x}$ y $N(x,y)=\frac{\delta F}{\delta y}$.
Solución de la EDs exactas
Para que la ecuación sea exacta, y pueda ser resuelta por éste método, es necesario que:
$$\frac{\delta M}{\delta y}=\frac{\delta N}{\delta x}$$
Si esta condición no se cumple naturalmente, a veces es posible multiplicar por un factor integrante para convertir una ecuación inexacta en una exacta.
Ejemplos resueltos
- $(y^2 e^{x y^2} + 4 x^3) d x + (2 x y e^{x y^2} – 3 y^2) d y = 0$
- $\left( x \sqrt{x^2 + y^2} – y \right) d x + \left( y \sqrt{x^2 + y^2} – x\right) d y = 0$
- $(x + 2 y) d x + (2 x + y) d y = 0$
- $\large ( 5x+4y ) d x+ ( 4x-8y^{3} ) d y=0$
- $( 2x y^{2} -3 ) d x+ ( 2x^{2} y+4 ) d y=0$
Para ver un desarrollo detallado sobre la técnica de soluición de las ecuaciones diferenciales exactas, revisa nuestro artículo: ECUACIONES DIFERENCIALES EXACTAS EJEMPLOS. (Ver tambien, al final del artículo para más ejemplos)
Las ecuaciones lineales y exactas comparten la propiedad de tener un mecanismo estructurado para encontrar una solución. Mientras que el mecanismo para las lineales está en el uso del factor integrante, para las exactas se basa en la existencia de una función potencial cuyas derivadas parciales describen el sistema.
Directa y por Sustitución
Directa

Forma estándar
Las ecuaciones diferenciales directas son aquellas que son conformadas por una sola derivada, que puede ser de primer orden o de orden superior y éta es igualada a una constante, constuyendo la siguiente forma estándar:
$$\frac{d^{n}y}{dx^{n}}=k$$
Donde n, puede ser cualquier número entero.
Éste tipo de ecuaciones se encuentra comúnmente en problemas físicos relacionados con movimiento. Un ejemplo que puede ilustrar el algorithmo de solución puede ser la siguiente:
$$\frac{d^{2}x}{dt^{2}}=k$$
que bien puede representar la aceleración de una partícula.
Solución de la EDs exactas
Su solución se encuentra al integrar iterativamante las derivadas anidadas, por ejemplo, para el caso anterior:
\begin{eqnarray*} \frac{d^{2}x}{dt^{2}}& = & k\\ \frac{d}{dt}\left(\frac{dx}{dt}\right) & = & k \end{eqnarray*}De modo que, integrando, tenemos:
\begin{eqnarray*} d \left( \frac{d x}{d t} \right) & = & k d t\\ \int d \left( \frac{d x}{d t} \right) & = & k \int d t + C\\ \frac{d x}{d t} & = & k t + C\\ d x & = & k t dt + C d t\\ \int d x & = & k \int t d t + C \int d t + C_1\\ x (t) & = & \frac{k}{2} t^2 + C t + C_1 \end{eqnarray*}Sustitución
Forma estándar
Las ecuaciones diferenciales por sustitucion de primer orden, tienen la formaestandar caracteristica:
$$\frac{dy}{dx}=f\left(Ax+By+C \right)$$
Donde: A,B,C, son constantes.
Solución de las EDs por sustitución
Las ecuaciones de éste forma, pueden ser siempre resueltas mediante reducirlas a variables separables con la sustitución
$$z=A x+B y+C$$
donde $B≠0$$
Ejemplos resueltos
- $\frac{d y}{d x} = (x + y + 1)^2$
- $\frac{d y}{d x} = \tan^2 (x + y)$
- $\frac{d y}{d x} = 2 + \sqrt{y – 2 x + 3}$
- $\frac{d y}{d x} = \cos (x + y)$
Ejemplos paso a paso de ecuaciones diferenciales resueltas por sustitución puedes encontrarlas en éste artículo: Ecuaciones diferenciales por sustitucion. Tambien puedes descargar la presentación de ése tema desde nuestra tienda online:

Riccati y Bernoulli
Bernoulli

Forma estándar
Una ecuación de Bernoulli es una ecuación diferencial no lineal que tiene la siguiente forma:
$$\frac{dy}{dx}+p(x)y=q(x)y^{n}$$
Donde: $\left( n\neq0, n\neq1\right)$
Solución de las EDs de Bernoulli
Estas se pueden resolver realizando un cambio de variable que la transforme en una ecuación lineal. La sustitución común es:
$$v=y^{1-n}$$
lo cual simplifica la ecuación de Bernoulli a una forma lineal.
Ejemplos resueltos
- $\begin{equation} \Large x \frac{d y}{d x} +y= \frac{1}{y^{2}} \end{equation}$
- $\begin{equation} \Large \frac{d y}{d x} -y=e^{x} y^{2} \end{equation}$
- $\begin{equation} \Large \frac{d y}{d x} =y ( x y^{3} -1 ) \end{equation}$
- $\begin{equation} \Large x \frac{d y}{d x} – ( 1+x ) y=x y^{2} \end{equation}$
- $\begin{equation} \Large t^{2 } \frac{d y}{d t} +y^{2} =t y \end{equation}$
Ambas, las ecuaciones de Ricatti y Bernoulli, ilustran las complejidades que pueden surgir con ecuaciones diferenciales no lineales. A diferencia de las lineales y exactas, estas pueden no tener soluciones que se expresen en términos de funciones elementales, pero la ecuación de Bernoulli es reducible a una forma lineal y tiene un método sistemático para su resolución.
Ejemplos desarrollados paso a paso se pueden ver en el artículo: Ecuaciones Diferenciales de Bernoulli.
Riccati

Forma estándar
La ecuación de Ricatti es una forma no lineal de ecuación diferencial de primer orden que se escribe comúnmente como:
$$\frac{dy}{dx}=q_0(x)+q_1(x)y+q_2(x)y^{2}$$
donde $q_0(x)$, $q_1(x)$, y $q_2(x)$ son funciones conocidas de x.
Solución de las EDs de Riccati
A menudo, estas ecuaciones no tienen una solución en términos de funciones elementales, a menos que tengamos una solución particular, en cuyo caso podemos reducirla a una ecuación de Bernoulli.
Teniendo una solución conocida: $y_1$, podemos realizar la transformación de la ED a un ED de Bernoulli, con la siguiente sustitución:
$$y = y_1 + u$$
donde $u(x)$, es una dunción de $x$, como se muestra.
Ejemplos resueltos
- $\frac{dy}{dx}-\left(1-x\right)y^{2}=\left(2x-1\right)y-x$
- $y’=\frac{y}{x}+x^{2}y^{2}-x^{4}$
- $y’=-y^{2}\sin{(x)}+2\tan{(x)}\sec{(x)}$
Ejemplos resueltos paso a paso de ecuaciones diferenciales de Riccati, pueden verlos en nuestro artículo: Ecuaciones Diferenciales No-Lineales: Riccati, Ejercicios Resueltos y Ecuaciones Diferenciales No-lineales: Riccati, Ejemplos Resueltos, que puedes encontrar en el blog de nuestra tienda online.
Ejemplos resueltos en python
Profundiza tu conocimiento y conviertete en un expert@ aprendiendo a resolver con software libre y potente tus ecuaciones diferenciales, te recomiendo adquieras nuetros códigos para resolver tus problemas en nuestra tienda online.
Ejercicios Resueltos Riccati con SageMath. – Domina la resolución de Ecuaciones de Riccati con códigos que te permiten obtener resultados inmediatos, masivos y reales

Lagrange y Clairaut
Lagrange

Forma estándar
Las ecuaciones diferenciales de Lagrange son un tipo especial de ecuaciones diferenciales de primer orden que se pueden representar en la forma de un problema de valores en la frontera:
$$y=xf\left(y’\right)+g\left(y’\right)$$
Solución de las EDs de Lagrange
Realizamos la sustitución:
$$y’=p$$
buscando poder aislar la derivada de la función dependiente, implicita, y obtrner una expresión del tipo $\frac{dy}{dx}=…$ que podamos integrar.
A veces, se resuelven encontrando una familia de soluciones, que podrían dar lugar a una solución en forma de una envolvente de una familia de curvas.
Sin embargo, no todas las ecuaciones de Lagrange tienen formas cerradas y podrían requerir métodos numéricos para su solución.
Ejemplos resueltos
- $y=x+y’-3(y’)$
- $y=2xy’-y^2$
- $y=\left(\cos{(y’)}+y’\right)x + \frac{1}{2}\sin{(y’)}\cos{(y’)}+\frac{1}{2}y’$
- $y=x\left(y’+3\right)-2\left(y’\right)^{2}$
- $y=x\left(y’\right)^{2}-y’$
Ejemplos resueltos paso a paso de ecuaciones diferenciales de Lagrange, pueden verlos en nuestro artículo: Ecuaciones Diferenciales de Lagrange, Ejercicios Resueltos. Disponible en nuestro blog.
Clairaut

Forma estándar
Las ecuaciones de Clairaut son un tipo de ecuación diferencial en el que la función y su derivada están relacionadas linealmente:
$$y=xy’+g(y’)$$
donde $g$ es una función conocida de $y’$.
Solución de las EDs de Clairaut
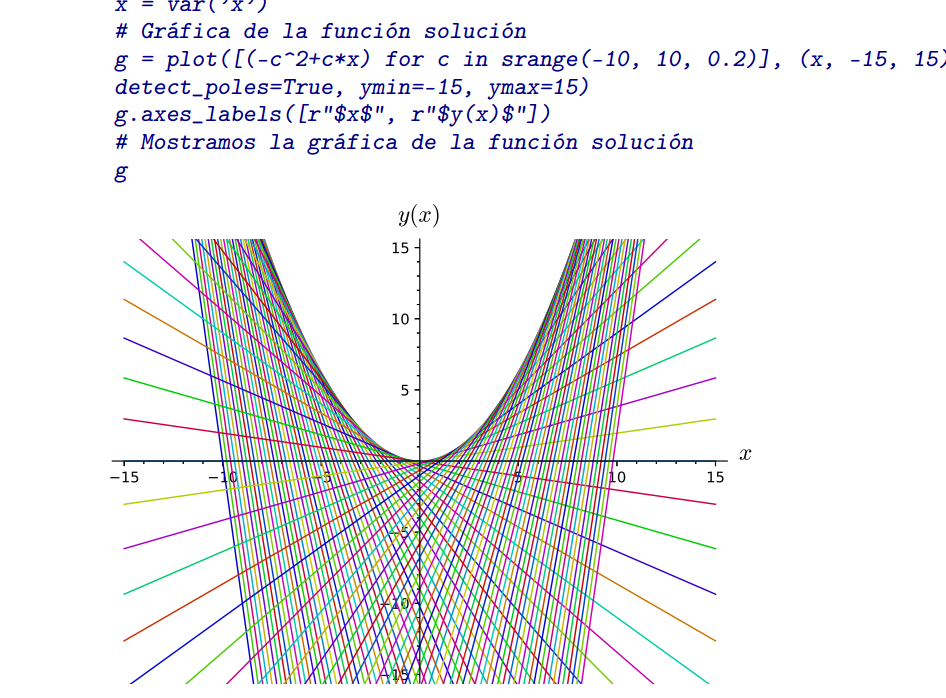
Una de las características interesantes de las ecuaciones de Clairaut es que tienen tanto una solución general como una solución singular. La solución general se compone típicamente de una familia de líneas rectas, mientras que la solución singular es la envolvente de estas líneas.
Ejemplos resueltos
- $y=xy’+(y’)^{3}$
- $\left( x^{2}-1\right)\left(y’ \right)^{2}-2xyy’+y^{2}=0$
- $y=xy’-\tan{y’}$
- $y=xy’+\frac{y’}{\sqrt{1+(y’)^{2}}} $
- $y – xy’=\frac{a}{2y’}$
Ejemplos resueltos paso a paso de ecuaciones diferenciales de Riccati, pueden verlos en nuestro artículo: Ecuacion Diferencial de Clairaut, Ejercicios Resueltos.
Ambas, las ecuaciones de Lagrange y las de Clairaut implican métodos de solución que buscan una relación implícita entre las variables y sus derivadas, contrastando con las ecuaciones separables o lineales que a menudo permiten una solución explícita más directa.
Las ecuaciones diferenciales de Lagrange y de Clairaut proporcionan ejemplos interesantes de cómo una ecuación diferencial puede tener soluciones que no necesariamente siguen un formato estándar, retando así a los métodos de solución tradicionales y ofreciendo oportunidades para una exploración matemática más profunda.
Comparaciones de los diferentes tipos de ecuaciones diferenciales ordinarias de primer orden
Tipos de ecuaciones diferenciales ordinarias de primer orden, lineales
Al comparar todos estos tipos de ecuaciones, las directas y separables son por lo general más directas de resolver, debido a que involucran manipulaciones algebraicas más simples y técnicas de integración básicas. Las lineales y exactas requieren métodos más estructurados y la aplicación de procedimientos como factores integrantes o la búsqueda de funciones potenciales, respectivamente.
La ecuaciones Homogéneas y por Sustitución requieren de una pericia especial en matemáticas al ser necesario el buen manejo del algebra, como el manejo de fraciones parciales, para la adecuación de las ecuaciones a formas más asequibles de manejar, así como el buen manejo de técnicas de integración de funciones racionales e integración por partes.
Tipos de ecuaciones diferenciales ordinarias de primer orden, no-lineales
Las ecuaciones de Bernoulli, aunque no lineales, permiten una transformación que las reduce a una ecuación diferencial lineal, lo que facilita su resolución. Ricatti, Lagrange y Clairaut se desvían de estos caminos más trillados, ofreciendo un territorio más complejo, a menudo requiriendo soluciones particulares o enfrentándonos con formas de solución más inusuales como las envolventes de una familia de curvas.
| EDs lineales | EDs no-lineales | EDs reducidas a lineales |
|---|---|---|
| Separable | Homogénea | Homog{enea |
| Lineal | Exacta | |
| Directa | Sustitución | Sustitución |
| Bernoulli | Bernoulli | |
| Riccati | Riccati | |
| Lagrange | ||
| Clairaut |
Resumen de los tipos de EDs ordinarias de primer orden, lineales y No-lineales, más importante.
Para poner estos conceptos en contexto académico y facilitar su aplicación, se compone un cuadro sinóptico que resume las características de cada una de las ecuaciones descritas anteriormente:
| Ecuación | Forma estándar | Método de solución |
|---|---|---|
| Separable | $\frac{dy}{dx}=g(x)h(y)$ | Separación de variables e integración |
| Homogénea | $\frac{dy}{dx}=f\left(\frac{y}{x}\right)$ | Sustitución y separación de variables |
| Lineal | $\frac{dy}{dx}+p(x)y=q(x)$ | Factor Integrante |
| Exacta | $M(x,y)dx+N(x,y)dy=0$ | Función potencial $F(x,y)$ |
| Directa | $\frac{dy}{dx}=c$ | Integración directa, donde $c=$ constante |
| Sustitución | $\frac{dy}{dx}=f\left(Ax+By+C\right)$ | Sustitución pertinente, ej.: $z=Ax+By+C$ |
| Bernoulli | $\frac{dy}{dx}+p(x)y=q(x)y^{n}$ | Sustitución $v=y^{1-n}$, ecuación lineal |
| Riccati | $\frac{dy}{dx}=q_0(x)+q_1(x)y+q_2(x)y^{2}$ | Solución particular o métodos numéricos |
| Lagrange | $y+xf\left(y’\right)+g\left(y’\right)=0$ | Análisis de soluciones singulares y generales |
| Clairaut | $y=xy’+g\left(y’\right)$ | Análisis de soluciones singulares y generales |
Este cuadro proporciona una vista rápida de los diferentes tipos de ecuaciones diferenciales de primer orden consideradas, junto con las formas estándar asociadas y las estrategias recomendadas para encontrar soluciones.
Cómo se clasifican las ecuaciones diferenciales ejercicios (video)
Conviertete en expert@

Continúa llevando tu conocimiento al siguiente nivel, te recomendamos nuestras herramientas y cursos exclusivos:
Ecuaciones Diferenciales 1er Orden Sagemath y Python Lineales y No-Lineales. – Conviertete en un Expert@ en la solución de todos los tipos de Ecuaciones Diferenciales ordinarias de primer orden, lineales y No-lineales, con sagemath y Python. Lleva tus habilidades al siguiente nivel, y moldea tu destino con compromiso y diciplina para desarrolar lo mejor de tí, adquiere nuestro artículo y sé un experto en resolver y varificar distintos escenerios para cualquier fenómeno físico que se representen con modelos matemáticos de EDs lineales y no lineales de 1er orden.
Si no adquiriste los códigos y quieres completar tu expertise, busca el código de descuento dentro del artículo y complementalo con le notebook de códigos el cual contiene mas ejemplos. Para accederlo búscalo en nuestra tienda online como: Sagemath y Python – Ecuaciones Diferenciales 1er Orden Lineales y No-Lineales (código)
Ecuaciones diferenciales e Inteligencia Artificial
Métodos de Estimación de Parámetros en Modelos No Lineales con Python – Conviértete en un experto en la estimación de parámetros para modelos dinámicos no lineales, utilizando las herramientas más avanzadas como Python y técnicas de Machine Learning. Lleva tus habilidades al siguiente nivel y construye un futuro profesional sólido, donde tu capacidad para resolver problemas complejos te distinga. Adquiere nuestro artículo y adquiere el dominio necesario para ajustar modelos a datos reales, realizar pronósticos precisos y simular diferentes escenarios en cualquier campo que requiera una comprensión profunda de sistemas no lineales. Es tu oportunidad para destacar y ser reconocido por tu compromiso y disciplina en la ciencia de los datos.

Explora nuestros Cursos Exclusivos en linea
¿Qué son las Ecuaciones Diferenciales? – Adéntrate en los fundamentos de las Ecuaciones Diferenciales y amplía tu perspectiva sobre su aplicabilidad.
Ecuaciones Diferenciales de Primer Orden – Perfecciona tus habilidades con nuestro curso especializado en Ecuaciones Diferenciales de Primer Orden.

Programa Completo: Ecuaciones Diferenciales, Modelado, Aplicaciones e Inteligencia Artificial (https://ecuacionesdiferencialesaplicaciones.com/membresias/ecuaciones-diferenciales-programa-completo-2/) – Descubre nuestro programa integral que abarca Ecuaciones Diferenciales, Modelado, Aplicaciones e Inteligencia Artificial. Un paso crucial hacia tu dominio en este campo.
Nuestros recursos están diseñados para aquellos que buscan alcanzar un nivel excepcional en Ecuaciones Diferenciales (e Inteligencia artificial) y elevarse al pináculo de su sector profesional, así como tambien para docentes y estudiantres comprometidos con su excelencia!. ¡Invierte en tu crecimiento académico y conviértete en un EXPERTO hoy!
¿Encontraste lo que buscabas?
¿Quiero una visión general desde cero? te recomiendo nuestro artículo: Domina las Ecuaciones Diferenciales Ordinarias: Guía Esencial 2024,
¿Quieres ejemplos sobre inteligencia artificial y ecuaciones diferenciales, revisa nuestro artículo: Cómo Resolver Ejercicios de Estimación de Parámetros en Sistemas No Lineales?
¿Quieres más profundidad en el conocimiento de las ecuaciones no-lineales de pimer orden? te recomiendo nuestros artículos:
